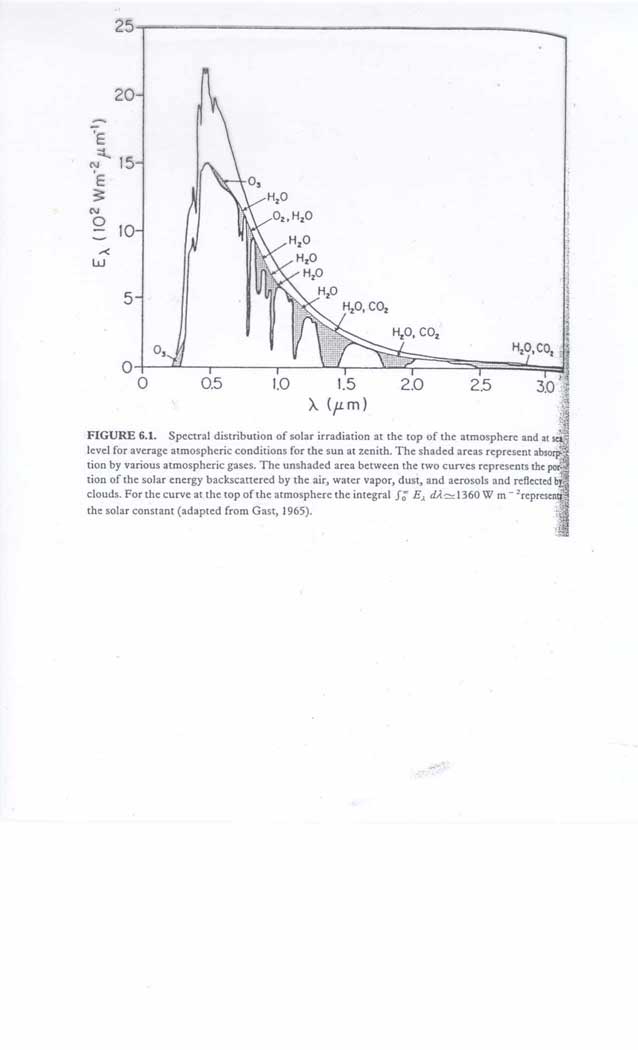
What determines the temperature on earth ? We will first look at global mean values of heat budgets and not too much at the latitudinal variation. Important variables are 1. solar energy input and spectral distribution; 2. atmospheric albedo; 3. surface albedo; 4. concentrations of greenhouse gases; 5. concentrations of short wavelength absorbers

The solar radiation energy at one astronomical unit (distance of earth to sun) is called the insolation constant S, about 1365 W/m²; we can assume that all that radiation arrives at the earth as a parallel beam. The earth intercepts as a disk with radius R on the order of 1.7 10¹⁷ watts, but that amount of energy is "smeared out" over its spherical surface. We can recalculate the average terrestrial insolation constant S* as S* = S xpR² / 4pR², where R is the earth radius. The amount of energy intercepted equals S times the surface of a disk with radius R; this energy is distributed over the surface of the earth sphere. The value of S* is S/4 = 340 W/m², obviously averaged over a 24 hour period. Physicists know a lot about radiative processes so a few physics laws follow:

All these considerations are for annual, whole-earth radiative balances. Now we are ready to look at zonal differences. The surface as well as the atmospheric albedo vary strongly as a function of latitude: snow reflects a lot more light than corn fields! In addition, the angle of incidence of the solar radiation varies as a simple function of latitude: the incoming energy is smeared over a larger surface area at higher latitudes and the albedo effects is also sensitive to angle of incidence. These are two reasons that the polar regions will have a much smaller absorbance of solar radiation. The terrestrial radiation also varies as a function of latitude, largely a reflection of the temperature. We can now subtract the terrestrial radiation from the net incoming radiation per latitude band and the result is a regional account of the radiative imbalance. We can approach this from the empirical side based on satellite measurements, resulting in fig. 4. The poles are losing heat, with the N pole losing more heat than the south pole. The oceans gain more heat than the landmasses, which sets up a condition for heat transfer from the oceans to land, especially during the winter. The total amount of heat transport from low latitudes to higher latitudes can be as high as 6 x 10¹⁵ W. Much of climatology deals with the distribution of heat over earth, which is obviously strongly tied to this zonal radiative balance. My "mastergraph" shows the combination of the radiation and convection budget of the earth. Try to understand these various balances and calculations, and you got it down. For the convective heat flow, about 50 % is done through sensible heat transport (warm air), 30% through latent heat transport (evaporation of water) and 20 % by the oceans.

Let us now look more in detail at the nature of the greenhouse effect. The incoming solar radiation has only a small amount of energy in the infrared bands, but the terrestrial radiation is largely within the infrared wavelengths. We can thus argue that a large part of the incoming solar radiation is transmitted through the atmosphere (apart from scattering, reflection, and short-wavelength absorption, etc) whereas a substantial part of the outgoing long-wavelength terrestrial radiation is absorbed. Absorption of the short (ultraviolet) wavelengths leads to electronic transitions, whereas infrared absorption leads to changes in the vibrational and rotational spectra of the molecules. Dimeric molecules are radiatively neutral but "things" with several arms can either change their rotational or vibrational energies.. The likelihood of absorption of a photon with the appropriate wavelength for a substance is labeled the absorption cross section.

Many molecules have several absorption bands, related to different vibrations and rotations. Important terrestrial greenhouse gases and their absorption spectrum are shown in figure 2. We can express this also in Te values for each wavelength (plotted here as the inverse of Te, % absorption in fig. 2). When we look at Te on a per wavelength basis we can see that some windows are very "dirty", with a Te close to zero. These dirty windows are caused by the infrared absorption of CO2 and H2O. There are "open" windows in the spectrum and that is where the bulk of the terrestrial radiation escapes through to outer space. It is intuitively clear that absorbers that act within these relatively clean windows will have a proportionally large effect on the total atmospheric transmissivity. Important absorbers in these open windows are methane (CH₄) and nitrous oxide (N₂O), which have overlapping absorption bands with each other.

We are now in the position to investigate the radiative effect of changes in the concentrations of greenhouse gases, the so-called radiative forcing of the greenhouse gases. The radiative forcing factors for some common greenhouse gases are given in table 2. The CO₂ and H₂O windows are already dirty, and so a little bit more CO₂ will not dramatically influence the radiative balance (flat end of the deBeer curve). The CO₂ radiative forcing thus scales with the logarithm of the gas concentration. The CFC's have several absorption bands and absorb in a virtually clean window of the natural atmosphere: their greenhouse forcing is therefore on a mole by mole basis very large compared to that of CO₂. Sometimes the greenhouse forcing is thus listed as the CO₂ equivalent greenhouse effect of a gas as applied to the modern atmosphere (Table 3). It is a common error in many low-level textbooks and newspaper articles to state that methane and CFC are much stronger greenhouse gases than CO₂, like if this were a material property (e.g., because they are much better absorbers that supposedly have a larger cross section and/or more absorption bands). The fact is, they absorb in a region of the spectrum where no other natural compounds absorb, and especially for the synthetic CFCs, the influence of each newly released molecule thus counts heavily. The CFCs do indeed have absorption bands with intensities about 10 times greater than CO₂ absorption at 15 micrometer (the main CO2 absorption band), but compare this with the CFC factors in Table 3. This short overview shows that the calculation of the total greenhouse effect with a changing atmospheric composition is not an easy thing, partially because of band overlap, and non-linear effects.

It is obvious from the foregoing that the greenhouse effect retains some of the radiated energy from the earth surface in the atmosphere: unidirectional radiation from the earth surface (outwards) is absorbed and re-radiated in all directions, including back to the surface. This re-radiated energy can be absorbed again and re-radiated once more. The earth surface will thus warm up as a result of the greenhouse effect. This radiative transport back and forth will not change the temperature of the atmosphere, however, which is a function of the kinetic energy of the main gas molecules, N₂ and O₂, which are neutral in radiative sense (do not absorb or emit long-wavelength fotons). How is the energy transferred from the trace greenhouse components to the main mass of gases? This is another one of those issues that is rarely addressed in detail in most textbooks. Realize that absorption of the quants of energy by greenhouse gas molecules only raises their internal energy. That process is not changing either their temperature or that of other gas molecules. The transfer of energy must partly occur in the short timespan between absorption and re-emittance of the infrared quants through molecular collisions. In the dense troposphere collisions are manifold and so a large amount of energy can be transferred to the "inert" main gas molecules (thermal equilibration). In addition, there is the convective heat transport from the earth surface into the atmosphere, so the back radiated heat from the greenhouse can be picked up by the atmosphere and convectively distributed.

A crude way of assessing the temperature effect of changes in either greenhouse forcing, albedo or solar intensity goes as follows:

When the green house gases increase in concentration more heat is trapped and we label that effect dF (the radiative forcing, or amounts of W/m² extra absorbed). This will result in a temperature increase and we can reason that process as follows: more greenhouse gases, less heat escapes to outer space (the 239 W/m²), the atmosphere heats up, and because of Boltzmann the atmosphere increases its radiation, so the 239 W/m² that goes out is restored. We can assume that the radiative forcing dF is linearly related to the resulting surface temperature change dT by some proportionality constant, or dT = b dF and b is sometimes called the climate sensitivity factor (= dT/dF). From Boltzmann we learned that F = s T⁴, so dF/dT = 4 s T³ (= 1/b). We can express b then conveniently as 1/ (4 sT³ ) which is equal to T/ 4 s T⁴ which is equal to T/4F. So if we know the outgoing radiation from the earth surface (F) and the associated surface temperature T, we can calculate the change in temperature for small changes in greenhouse gas concentrations according to dT = T(old)/4F(old) dF. The current values of b is about 0.3 C per W/m² unit change. The dF values we can calculate from de Beer's Law knowing k, height of the atmosphere and putting in the changes in greenhouse gas concentrations. Some of these expressions are given in table .